

Tyypillisimmät algoritmit ja niiden käyttötarkoitukset
Tämä artikkeli on toinen osa Martti Asikaisen ja Janne Kauttosen kirjoittamasta sarjasta ”Mitä algoritmit ovat ja mitä sinun tulisi niistä tietää”. Tässä osassa syvennymme algoritmien teknisempiin käsitteisiin. Ensimmäisen osan löydät täältä.
Martti Asikainen & Janne Kauttonen, 22.3.2025
Algoritmit ovat keskeinen osa modernia teknologiaa. Ne toimivat kuin tarkat ohjeet, jotka suorittavat ennalta määrättyjä tehtäviä vaihe vaiheelta. Yksinkertaisimmillaan algoritmi voi järjestää luvut numerojärjestykseen, kun taas monimutkaisimmillaan ne ohjaavat tekoälyn toimintaa ja vaikuttavat jopa siihen, millaista sisältöä meille suositellaan verkossa. Tässä artikkelissa syvennymme erilaisiin algoritmityyppeihin ja niiden käyttökohteisiin. Aloitamme hakualgoritmeista, jotka ovat yksinkertaisimpia mutta samalla monipuolisimpia algoritmeja – niitä käytetään lähes kaikissa ohjelmissa, jotka käsittelevät tietoa.
Hakualgoritmit jaetaan tyypillisesti lineaariseen hakuun ja binäärihakuun. Lineaarinen haku käy järjestelmällisesti läpi jokaisen taulukon alkion, kunnes haluttu arvo löytyy (Cormen et al., 2009). Binäärihaku puolestaan toimii kuin sanakirjan selaaminen: se aloittaa haun keskeltä ja rajaa hakualuetta jatkuvasti puoleen suuntaamalla etsinnän joko alku- tai loppupäähän. Binäärihaku edellyttää kuitenkin, että data on valmiiksi järjestetty joko nousevaan tai laskevaan järjestykseen (Knuth, 1998; Grossman & Frieder, 2004). Käytännössä tämä tarkoittaa sitä, että tiedot on ensin lajiteltava, mutta sen jälkeen binäärihaku on huomattavasti nopeampi kuin lineaarinen haku.
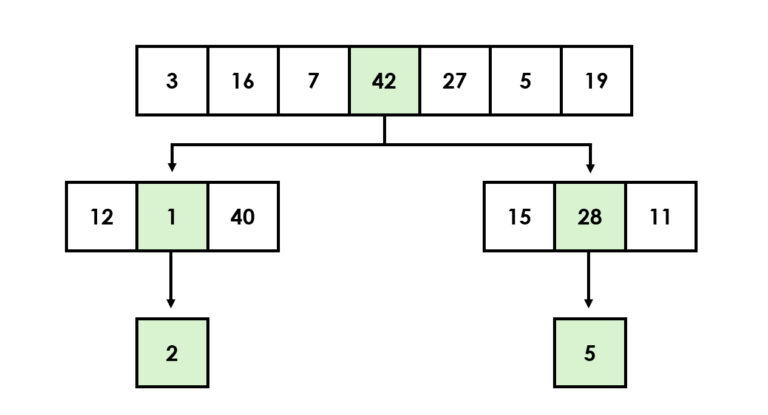
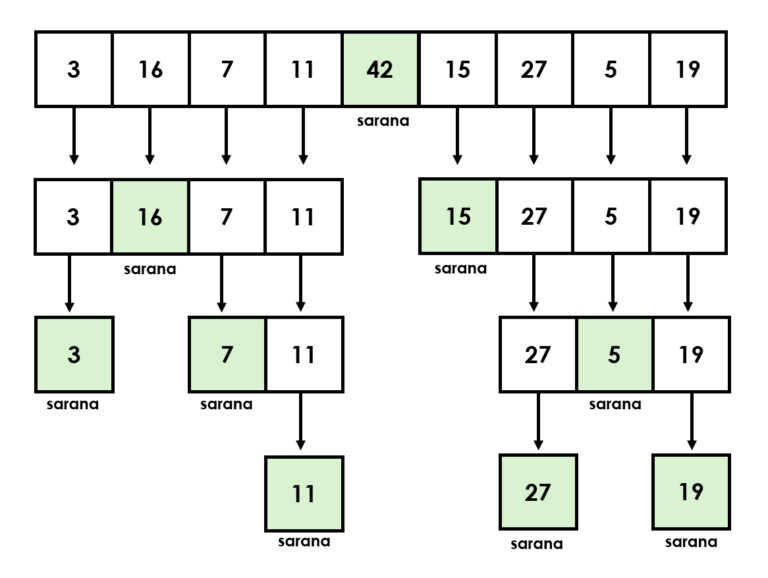
Lajittelualgoritmit taistelevat kaaosta vastaan luoden järjestystä tietorakenteisiin vertailevan operaattorin avulla. Yksi tunnetuimmista lajittelualgoritmeista on pikajärjestys (quicksort), joka hyödyntää hajota ja hallitse -periaatetta jakamalla tietojoukon pienempiin osiin ja käsittelemällä ne rekursiivisesti (Hoare, 1962).
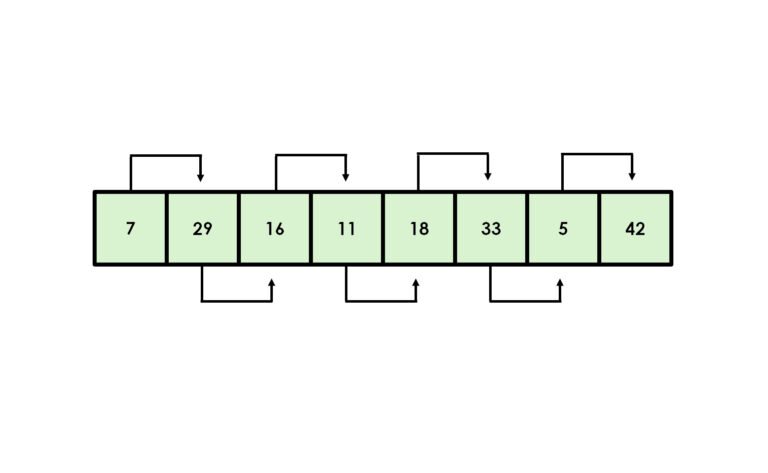
Toinen tehokas lajitteluperuste on lomituslajittelu (eng. merge sort), joka yhdistää osajoukkoja järjestyksessä (Cormen ym. 2009). Myös yksinkertaisemmat algoritmit, kuten esimerkiksi kuplalajittelu (eng. bubble sort) ja valintalajittelu (eng. selection sort) voivat olla hyödyllisiä. Toisaalta asiantuntijoiden mukaan ne sopivat lähinnä opetustarkoituksiin ja visuaaliseen esittämiseen (Sedgewick & Wayne, 2011).
Lomituslajittelulla listat kuntoon
Edellä käsiteltyjen binäärisen haun ja pikajärjestyksen tapaan myös lomituslajittelu on nk. rekursiivinen algoritmi, joka venäläisen maatuskanuken tapaan pitää sisällään pienempiä versioita itsestään. Rekursioissa on aina kaksi osaa, jotka ovat perustapaus eli tilanne, jossa vastaus on tiedossa, sekä rekursiivinen tapaus, joka ratkaistaan pilkkomalla. Tästä syystä niitä kutsutaan myös hajoita ja hallitse -algoritmeiksi, suurten ongelmien kesyttäjiksi, jotka pilkkovat ison ongelman pienemmiksi palasiksi ja ratkovat niitä, kunnes koko tehtävä on valmis.
Toinen käytännön esimerkki voisi olla tilanne, jossa tiedostosi ovat sekaisin. Täysin hujan hajan, ja että haluaisit saada ne järjestykseen algoritmin avulla. Rekursiivinen algoritmi avaisi ensin pääkansion, menisi ensimmäiseen alakansioon ja sen alakansion alakansioon järjestääkseen sen perusehdossa määrätyllä tavalla. Alimmasta kansiosta se siirtyisi aina ylemmäs kansiopuuta kavuten, samaa periaatetta hyödyntäen, kunnes kaikki tiedostot olisivat järjestyksessä, jonka jälkeen se siirtyisi seuraavaan kansioon. Tätä periaatetta hyödynnetään esimerkiksi tiedostonhallinnassa sekä verkkosivujen rakenteissa.
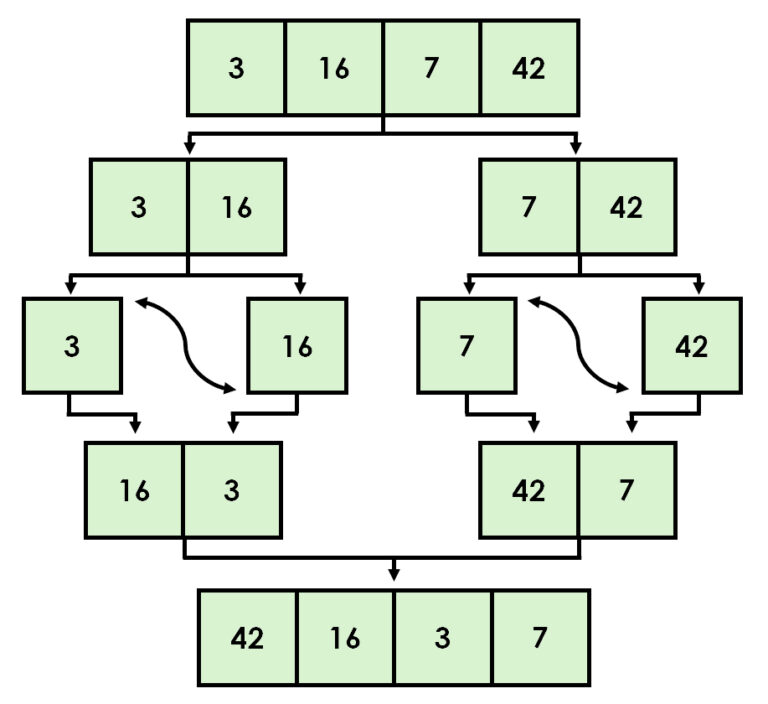
Yksi lomituslajittelun merkittävistä eduista on sen kyky toimia tehokkaasti linkitetyissä listoissa ilman ylimääräisen muistitilan tarvetta. Sen käyttö ei kuitenkaan rajoitu vain yksinkertaiseen järjestämiseen. Sitä voidaan hyödyntää myös inversioiden laskemiseen listassa, mikä on hyödyllistä esimerkiksi tietorakenteiden analysoimisessa tai järjestämistoimenpiteiden monimutkaisuuden arvioimisessa.
Lisäksi lomitusjärjestäminen on erinomainen valinta ulkoiseen järjestämiseen, jossa käsitellään niin suuria tietomääriä, etteivät ne mahdu kerralla tietokoneen muistiin. Erityisen arvokas se on kuitenkin tilanteissa, joissa tiedon stabiiliudella on merkitystä. Stabiilissa järjestämisessä samanarvoiset alkiot säilyttävät alkuperäisen keskinäisen järjestyksensä myös lajittelun jälkeen, mikä parantaa tiedon luettavuutta ja käytettävyyttä.
Kuvitellaan esimerkiksi taulukkoa, jossa henkilöt on ensin järjestetty nimen mukaan ja sen jälkeen ne halutaan järjestää ikäryhmittäin. Lomituslajittelun avulla samanikäiset henkilöt pysyvät edelleen aakkosjärjestyksessä.
Klusteroinnista potkua segmentointiin
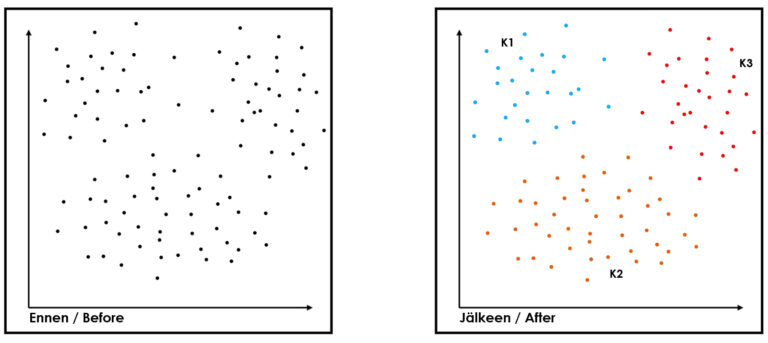
Segmentoinnista puhuttaessa ei voi ohittaa k-means klusterointia, joka on yksi yleisimmistä ja yksinkertaisimmista ohjaamattoman koneoppimisen klusterointialgoritmeista. kuuluu ohjaamattoman koneoppimisen menetelmiin. Sen tarkoituksena on jakaa datajoukko ennalta määrättyyn k-määrään ryhmiä eli klustereita, joissa havainnot ovat mahdollisimman samankaltaisia keskenään (esim. MacQueen 1967). Sitä voi hyödyntää esimerkiksi kuvantunnistamiseen, asiakassegmentointiin ostokäyttäytymisen, demograafisten tietojen tai verkkokäyttäytymisen perusteella.
Muita käyttötarkoituksia ovat esimerkiksi dokumenttien luokittelu, hinnoittelustrategioiden luominen (optimaaliset hintatasot eri segmenteille), anomalioiden eli epätavallisten tapahtumien tunnistaminen (pankit, finanssiala, tutkimus), henkilöstöanalytiikka (työntekijäprofiilit ja osaamistarpeet), inventaarion hallinta (tuotteiden ryhmittely myynnin, kausivaihtelun tai varastokierroksen perusteella), suosittelujärjestelmät (samankaltaiset asiakkaat tai tuotteet) sekä markkina-analyysit (kilpailevat yritykset tai markkina-alueet).
Päivittäistavarakauppa puolestaan voisi soveltaa klusterointia esimerkiksi siten, että tuotteet klusteroidaan kuluttajien ostokäyttäytymisen mukaan, jonka jälkeen kaupassa tuotteet järjestellään klusteroinnin perusteella. K-means klusteroinnin rajoituksiksi voidaan todeta, että ne toimivat parhaiten pallomaisilla klustereilla ja tulokset riippuvat alkuperäisten keskipisteiden valinnasta. Lisäksi se on herkkä poikkeaville havainnoille ja sen toiminta vaatii k:n eli klusterien lukumäärän määrittämisen etukäteen.
Graafialgoritmin käyttötarkoitukset
Tiedostonhallinnasta puhuttaessa on olennaista ymmärtää myös graafitietokantojen perusteet, sillä graafit tarjoavat luontaisen tavan esittää verkottunutta tietoa. Graafitietokannat järjestävät tiedon graafitietomallin mukaisesti, jossa solmut (eng. nodes) ja niiden väliset yhteydet tai kaaret (eng. edges) näkyvät selkeänä tietorakenteena (Angles & Gutierrez 2018). Tämä mahdollistaa datan luonnollisen mallinnuksen sen sijaan, että datapisteitä käsiteltäisiin toisistaan erillisinä. Solmuilla ja yhteyksillä voi olla monia eri ominaisuuksia, jotka sisältävät lisäinformaatiota – jokainen solmu tai yhteys kuvastaa jotain toista ominaisuutta tietokannassa. Graafi mahdollistaa monia operaatioita, jotka ovat työläitä esimerkiksi yksinkertaiselle datan taulukkorakenteelle. Esimerkiksi toisiinsa kytkeytyvien tietojen löytäminen on helppoa graafitietomallissa.
Tänä päivänä monet tunnetut yritykset vannovat graafitietokantojen ja -algoritmien nimeen niiden ketteryyden, skaalautuvuuden ja suorituskyvyn vuoksi. Eduksi voidaan laskea myös niiden soveltuvuus verkottuneelle datalle sekä kyky paljastaa monimutkaisia, usein piilossa olevia, yhteyksiä eri tietojen välillä. Tämä lisää selitysvoimaa esimerkiksi erilaisissa analyyseissä, jotka vaativat visualisointiominaisuuksia. Muita vahvuuksia ovat esimerkiksi tietokantakaavion joustavuus ja graafitietomallin ymmärrettävyys (esim. Thitz 2023). Graafitietomallia sovelletaan etenkin sosiaalisen median, semanttisen webin ja biologian aloilla (Barceló ym. 2011).
Vaikka graafitietokantoihin pohjautuvat algoritmit saattavat kuulostaa vierailta, niin törmäät niihin todennäköisesti päivittäin. Tutut sovellukset kuten Instagram, Facebook ja X hyödyntävät graafialgoritmeja yhdistääkseen käyttäjiä, heidän mieltymyksiään ja kartoittaakseen suosituksia. Myös Googlen alkuperäinen hakukone perustui PageRank-nimiseen graafialgoritmiin. Graafialgoritmit ovatkin varsin varteenotettava vaihtoehto perinteisille taulukoille ja relaatiotietokantapohjaisille ratkaisuille.
Ahneet algoritmit eli reitit aina Dijkstrasta primiin
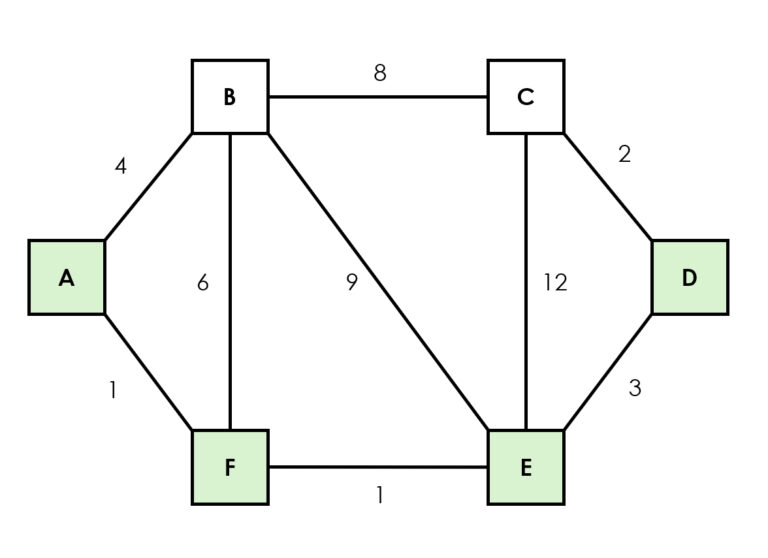
Reitinhakualgoritmit ovat tärkeitä graafiteoriassa ja suorastaan välttämättömiä verkostojen käsittelyssä. Dijkstran algoritmi on yksi käytetyimmistä reitinhakualgoritmeista lyhimmän polun löytämiseksi graafissa (esim. Google Mapsin liikkeen optimointi), missä kaikkien kaarien painot ovat ei-negatiivisia (Dijkstra, 1959). Muita reitinhakualgoritmeja ovat esimerkiksi Prim, joka rakentaa verkkoa lisäämällä lyhimpiä yhteyksiä uusiin solmuihin, Kruskal, joka valitsee aina lyhimmän mahdollisen yhteyden siten, ettei yhteydestä muodostu silmukkaa.
A-tähti-algoritmi (eng. A*) on laajennettu versio Dijkstran algoritmista ja sitä käytetään erityisesti peleissä ja navigointisovelluksissa, joissa halutaan nopeuttaa optimaalisen reitin löytämistä lähtöpisteestä (tai solmusta) muihin pisteisiin heuristiikkaa, kuten esimerkiksi euklidista metriikkaa ja Manhattan-etäisyyttä, hyödyntäen (Hart ym. 1968).
Dijkstra, A*, Prim ja Kruskal luokitellaan toisinaan myös niin kutsuttuihin ahneisiin algoritmeihin, joihin kuuluvat myös sellaiset algoritmit kuin ajoituksen optimointi (eng. activity selection problem), tiedonpakkaamiseen käytetty Huffmanin koodaus (eng. huffman coding) ja vaihtorahaongelma (eng. coin change greedy approach), jossa algoritmi antaisi vaihtorahan aina suurimmilla mahdollisilla yksiköillä.
Ahneet algoritmit toimivat kuin lapset karkkikaupassa. Ne tekevät joka askeleella sen hetkisen tiedon perusteella parhaalta vaikuttavan valinnan. Niissä ei myöskään ole jälkiprosessointia (eng. backtracking), joten ne eivät koskaan peruuta tekemiään valintoja, vaikka ne osoittautuisivatkin kokonaisuuden kannalta huonoiksi, koska ne muodostavat ratkaisun askel askeleelta. Ahneiden algoritmien keskeisimmäksi haasteeksi nouseekin löytää niille sopiva käyttötarkoitus, jossa ahne strategia tuottaa optimaalisen ratkaisun. Ongelman on oltava sellainen, että kulloinkin parhaalta näyttävä valinta tuottaa myös parhaan kokonaisuuden. Toisaalta ahne algoritmi on nopea ja helppo laskea, joten se voi olla varteenotettava vaihtoehto tilanteessa, jossa ratkaisun ei tarvitse olla optimaalinen.
Reitinhakualgoritmeista puhuttaessa on aiheellista mainita myös Bellman-Fordin algoritmi, joka laskee kaikkien solmujen lyhimmät etäisyydet yhdestä solmusta, ja jota hyödynnetään esimerkiksi taloudellisten kustannusten optimoinnissa, sekä etenkin liikeanalyysissä hyödynnettävä, dynaamiseen ohjelmointiin perustuva Floyd-Warshallin algoritmi, joka laskee kaikkien solmujen väliset lyhimmät etäisyydet. Se sopii erityisesti tiheisiin graafeihin ja sellaisiin tilanteisiin, joissa halutaan tietää solmujen välinen minimikustannus.
Väsytystaktiikkaa ja dynaamista ohjelmointia
Väsytysalgoritmi (eng. brute force) on hyödyllinen stressitesteihin, mutta sitä käytetään myös salasanojen, kirjautumistietojen ja salausavainten murtamiseen. Väsytysalgoritmi on sitkeä kuin kassakaappivaras, joka kokeilee ja kuulostelee jokaista eri yhdistelmää oven avaamiseksi. Se ei ole kovin taitava, vaan pikemminkin digitaalinen sisupussi, joka luottaa puhtaaseen periksiantamattomuuteen. Samalla se on kenties yksinkertaisin ja perusmuotoisin algoritmi, ja siksi myös varsin tehoton monimutkaisissa ongelmissa.
Väsytysalgoritmin toimintaperiaate on yksinkertainen. Esimerkiksi jos puhelimesi olisi lukittu nelinumeroisella PIN-koodilla, ja haluaisit avata sen hyödyntämällä väsytysalgoritmia, niin algoritmi kävisi läpi jokaisen mahdollisen vaihtoehdon 0000-9999 (0001, 0002, 0003…) välillä avatakseen sen. Algoritmia voi käyttää myös optimointiin ja reitinetsintäongelmiin (esim. kauppamatkustajan ongelma, TSP), jossa haetaan lyhintä reittiä eri kohteiden välillä.
Kauppamatkustajan ongelmassa (eng. traveling salesman problem) kauppamatkustaja tietää kaupunkien keskinäiset etäisyydet. Kysymys kuuluu, miten hän voi laskea itselleen nopeimman (lyhimmän, halvimman) kulkureitin, jossa käydään kaikkien solmujen kautta vain yhden kerran, ja palataan lopuksi lähtöpaikkaan. Väsytysalgoritmilla tämä tapahtuu siten, että lasketaan reittien kokonaismäärä, jonka jälkeen luetteloidaan kaikki mahdolliset reitit. Tämän jälkeen lasketaan kunkin reitin etäisyys ja valitaan lopuksi lyhin mahdollinen olemassa oleva reitti. Mikäli kaupunkeja on paljon (luokkaa 30), ongelma paisuu valtavaksi ja parhaankin supertietokoneen laskentateho loppuu kesken väsytysalgoritmia käytettäessä.
Dynaaminen ohjelmointi on menetelmä, jossa monimutkaisia ongelmia ratkaistaan jakamalla ne pienempiin osiin ja tallentamalla välituloksia, jotta samoja laskutoimituksia ei tarvitse tehdä toistuvasti. Ne eroavat perinteisistä hajota ja hallitse -algoritmeista siten, että dynaamisen ohjelmoinnin algoritmi jakaa ongelman päällekkäisiin osiin ja käyttää aikaisemmin laskettuja tuloksia tallentamalla ne uudestaan, kun taas hajota ja hallitse -algoritmit jakavat ongelman itsenäisiin osiin, jotka se ratkaisee erikseen ja yhdistää lopputuloksen.
Toisin sanoen dynaamisen ohjelmoinnin algoritmit ovat kuin kokeneita palapelin rakentajia, jotka oppivat helposti tunnistamaan toistuvat kuviot. Ne pilkkovat monimutkaisen ongelman pienempiin osiin ja osittain päällekkäisiin paloihin, ja kun yhden palan ratkaisu on löytynyt, niin ne tallentavat vastauksen muistiinsa myöhempää käyttöä varten. Ratkaisu onkin mitä sopivin moniin klassisiin tietojenkäsittelyn haasteisiin, kuten esimerkiksi reppuongelmaan (eng. knapsack problem), Fibonacci-lukujen laskemiseen (jokainen luku on edellisen kahden summa: 1,1,2,3,5,8…), jolloin algoritmi tallentaa jo lasketut arvot (memoization/tabulation), ja välttää tällä tavoin turhan laskennan (esim. Bellman, 1957; Cameron 1994; Brualdi 2005).
Dynaamisen ohjelmoinnin algoritmia käytetäänkin ennen kaikkea optimointiin. Se säästää laskenta-aikaa ja parantaa siten merkittävästi tehokkuutta. Jos samoihin ongelmiin vastattaisiin hajota ja hallitse -tyylillä ja puhtaasti rekursiivisesti, niin laskentatapa olisi varsin tehoton, koska samat arvot lasketaan useita kertoja. Muita yleisesti tunnettuja ongelmia, joihin dynaaminen ohjelmointi tarjoaa ratkaisun ovat pisimmän yhteisen osajonon ongelma (eng. longest common subsequence, LCS), matriisiketjun kertolasku (eng. Matrix Chain Multiplication), kolikkojen vaihto-ongelma (eng. Coin Change Problem) ja muokkausetäisyysongelma (eng. Edit Distance, esim. Levenshtein-etäisyys).
Satunnaistamista ja takaisinkytkentää
Yleensä ohjelmoinnissa ja algoritmien yhteydessä prosessien halutaan etenevän aina tarkan suunnitelman mukaan ilman yllätyksiä. Sattuma ja satunnaisuus ovat kuitenkin oleellinen osa lukuisia nykyaikaisia sovelluksia ja laskentamenetelmiä. Satunnaistetut algoritmit (eng. randomized algorithms) muodostavat oman erillisen algoritmikategoriansa, joka hyödyntää satunnaisuutta osana ongelmanratkaisuprosessia. Ne eivät suoraan kuulu perinteisiin algoritmikategorioihin, vaan ovat pikemminkin suunnittelutekniikka, jota voidaan soveltaa monenlaisiin algoritmeihin.
Niille on ominaista, että ne luottavat onneen ja sattumaan hyödyntämällä hallittua satunnaisuutta osana logiikkaansa ja vähentääkseen siten suoritusaikaa sekä yksinkertaistaakseen ongelmien monimutkaisuutta. Esimerkiksi aikaisemmin mainittu quicksort-järjestämisalgoritmi valitsee satunnaisen vertailukohdan (pivotin), mikä johtaa usein parempaan suorituskykyyn kuin kiinteän arvon käyttäminen.
Satunnaistetut algoritmit voidaan jakaa kahteen pääryhmään: Monte Carlo -algoritmeihin, jotka saattavat tuottaa virheellisen tuloksen tietyllä todennäköisyydellä, sekä Las Vegas -algoritmeihin, jotka tuottavat aina oikean tuloksen, mutta niiden suoritusaika vaihtelee. Satunnaistettuja algoritmeja käytetään usein tilanteissa, joissa tarkan ratkaisun löytäminen olisi liian hidasta tai monimutkaista, joten pitää tyytyä arvioon, joka on riittävän lähellä tarkkaa arvoa.
Niitä sovelletaan esimerkiksi kryptografiassa, numeerisessa integroinnissa, optimointiongelmissa ja tietojen tilastollisessa analysoinnissa. Satunnaistaminen tarjoaa ratkaisun moneen käytännön ongelmaan, joilla ei välttämättä löydy yhtä oikeaa optimaalista ratkaisua.
Esimerkiksi moni ravintola käyttää satunnaistettua algoritmia ruuhka-aikojen tilausten käsittelyyn. Sen sijaan, että tilaukset käsiteltäisiin saapumisjärjestyksessä, joka voisi johtaa pullonkauloihin tiettyjen annosten kohdalla, algoritmi arpoo satunnaisesti seuraavan valmistettavan tilauksen niiden joukosta, jotka ovat odottaneet pisimpään. Tämä vähentää keskimääräistä odotusaikaa ja pitää keittiön tasaisen työllistettynä.

Takaisinkytkentäalgoritmit puolestaan kuuluvat iteratiivisten algoritmien kategoriaan. Ne ovat tyypillisesti osa dynaamisia järjestelmiä tai koneoppimista, missä aiempien suorituskertojen tuloksia käytetään syötteenä seuraavilla suorituskerroilla. Toisin sanoen ne oppivat ja mukautuvat aiempien suoritusten tuloksista.
Tarkemmin määriteltynä takaisinkytkentäalgoritmit voidaan luokitella säätö- ja kontrollialgoritmeihin, joissa systeemin ulostuloa tarkkaillaan ja käytetään säätämään tulevia syötteitä (eng. control), järjestelmän aiempien tulosten perusteella suorituskykyään parantaviin oppiviin algoritmeihin (eng. learning) sekä optimointialgoritmeihin (eng. optimizing), jotka pyrkivät iteratiivisesti löytämään parhaan mahdollisen ratkaisun käyttämällä aiempia tuloksia.
Käytännön esimerkkejä takaisinkytkentäalgoritmien sovelluksista ovat neuroverkkojen takaisinvetoalgoritmi (eng. backpropagation), PID-säätimet sekä geneettiset algoritmit. Ne eroavat jäljitysalgoritmeista (eng. back-tracking algorithms) esimerkiksi siten, että jäljitysalgoritmit rakentavat ratkaisua inkrementaalisesti ja perääntyvät kun huomaavat, ettei nykyinen polku johda toivottuun ratkaisuun, kun taas takaisinkykentäalgoritmi oppii virheistään.
Tämän voi hahmottaa esimerkiksi kuvittelemalla labyrintin, josta pyrimme ulos algoritmin avulla. Jäljitysalgoritmi kävisi systemaattisesti koko labyrintin läpi, ja peruuttaisi aina törmätessään umpikujaan, kun taas takaisinkytkentäalgoritmi voisi opetella labyrintin rakenteen ulkoa aiempien yritystensä perusteella ja parantaa suorituskykyään jokaisen yrityksen jälkeen.
Molemmille algoritmeille on oma aikansa ja paikkansa. Jälitysalgoritmin systemaattinen lähestymistapa esimerkiksi sopii mainiosti monimutkaisten pulmien ratkaisemiseen ja peliteollisuuteen. Sitä käytetään löytämään ratkaisuja sudoku-pulmiin, tekoälyvahvisteisiin shakkipeleihin, molekyylien mallintamiseen sekä robottien liikeratojen suunnitteluun.
Takaisinkytkentäalgoritmit taas ovat mullistaneet neuroverkkojen kentän ja tehneet syväoppimisesta mahdollista. Klassisia takaisinkytkentäpulmia ovat esimerkiksi Hamiltonin sykli, joka kulkee verkon jokaisen pisteen kautta täsmälleen kerran (kts. kauppamatkustajan ongelma) sekä Ikean tavarataloillekin tyypillinen rotta labyrintissa -ongelma, jossa pyritään löytämään tie ulos, kun kaikki käytävät näyttävät samalta.
Yhteenveto ja johtopäätökset
Nyt olet lukenut kaksiosaisen artikkelimme ”Mitä algoritmit ovat ja mitä sinun tulisi niistä tietää”. Algoritmien tekninen tarkastelu paljastaa monipuoliset laskennalliset menetelmät, jotka ohjaavat modernia teknologiaa, ja muodostavat siten koko digitaalisen yhteiskuntamme näkymättömän selkärangan.
Perustason haku- ja lajittelualgoritmit jäsentävät tietoa, kun taas klusterointimenetelmät segmentoivat asiakkaita tehokkaammin. Graafialgoritmit mahdollistavat monimutkaisten suhteiden mallintamisen, ja reitinhakualgoritmit optimoivat reittejä verkostoissa. Kehittyneemmät lähestymistavat, kuten dynaaminen ohjelmointi, puolestaan ratkaisevat monimutkaisia ongelmia tallentamalla välituloksia, kun taas satunnaistetut ja palautemekanismeihin perustuvat algoritmit tuovat mukautuvuutta ja itseoppivia ominaisuuksia.
Toimialakohtaisia mahdollisuuksia on rajattomasti. Siinä missä k-means klusterointi jakaa asiakkaat ostokäyttäytymisen perusteella tehden markkinoinnista täsmällisempää, niin suosittelualgoritmit kasvattavat verkkokaupan keskiostosta tarjoamalla personoituja tuotesuosituksia. Koneoppivat algoritmit puolestaan ennakoivat sesonkivaihteluita ja menekkiä parantaen varastonhallintaa, kun taas reitinhakualgoritmit optimoivat logistiikkaa tuoden säästöjä kuljetuskustannuksiin ja tukien ympäristövastuullisuutta. Tämä osoittaa, että matemaattiset periaatteet on mahdollistaa muuntaa konkreettisiksi liiketoimintahyödyiksi, kun niitä käytetään oikein.
Pk-yrityksille algoritmien
käyttöönotto ei vaadi suuria alkuinvestointeja tai syvällistä teknistä
osaamista. Monet digitaaliset alustat ja ohjelmistot sisältävät valmiiksi
kehittyneitä algoritmeja, joita voi ottaa käyttöön ilman koodaustaitoja:
- Datan kerääminen ja organisointi. Algoritmien tehokkuus riippuu käytettävissä olevan datan laadusta ja määrästä. Asiakastiedot, myyntitilastot ja tuotekohtaiset tiedot muodostavat arvokkaan perustan.
- Pilvipohjaiset analytiikkatyökalut tarjoavat kustannustehokkaita ratkaisuja pk-yrityksille. Microsoft Power BI, Google
Analytics ja monet toimialakohtaiset ohjelmistot sisältävät valmiita algoritmeja, jotka voidaan ottaa käyttöön ilman merkittäviä IT-investointeja. - Ketterä kokeilu ja oppiminen on avainasemassa. Aloita pienestä, esimerkiksi yhden tuoteryhmän tai markkinasegmentin
algoritmisesta analyysistä, ja laajenna käyttöä tulosten perusteella.
Tulevaisuudessa algoritminen päätöksenteko vain vahvistuu, ja sen merkitys kilpailukyvylle korostuu entisestään. Pk-yrityksille on ensiarvoisen tärkeää pysyä kehityksessä mukana, sillä algoritmit tarjoavat mahdollisuuden toimia ketterämmin ja tehokkaammin kuin kilpailijat.
Tämä kirjoitus on julkaistu osana Haaga-Helia ammattikorkeakoulun Kone johtajana – tekoäly asiantuntija ja tietotyön johtamisessa -hanketta (2025-2026), jonka rahoittajana toimii Työsuojelurahasto.
Ota yhteyttä

Janne Kauttonen
Vanhempi tutkija
+358 294471397
janne.kauttonen@haaga-helia.fi

Martti Asikainen
TKI-viestinnän asiantuntija
+358 44 920 7374
martti.asikainen@haaga-helia.fi
Lähteet
Angles, R. & Gutierrez, C. (2018). An introduction to graph data management. In Fletcher, G., Hidders, J. & Larriba-Pey, J. L. (eds.), Graph Data Management, 1–32. Springer International. Cham.
Barceló, P., Libkin, L. & Reutter, J. (2011). Querying graph patterns. Proceedings of the Thirtieth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, 199–210.
Bellman, R. (1957). Dynamic programming and stochastic control processes. Information and Control 1 (3), 228-239. Elsevier. Amsterdam.
Brualdi, R.A. (2005). Introductory Combinatorics. 5th edition. Pearson. Lontoo.
Cameron, P. (1994). Combinatorics: Topics, Techniques, Algorithms. Cambridge University Press. Cambridge.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms (3rd ed.). MIT Press. Cambridge.
Dijkstra, E. W. (1959). A note on two problems in connexion with graphs. Numerische Mathematik, 1(1), 269–271. Springer.
Grossman, D. A. & Frieder, O. (2004). Information retrieval: algorithms and heuristics. (Second edition) Dordrecht: Springer.
Hart, P. E., Nilsson, N. J. & Raphael, B. (1968). A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Transactions on Systems Science and Cybernetics, 4 (2).
Hoare, C. A. R. (1962). Quicksort. The Computer Journal, 5(1), 10–16.
Knuth, D. E. (1998). The Art of Computer Programming, Volume 3: Sorting and Searching (2nd ed.). Addison-Wesley. Boston.
MacQueen, J. (1967). Some methods for classification and analysis of multivariate observations. Berkeley Symp. on Mathematical Statistics and Probability, 1, 281-297.
Sedgewick, R., & Wayne, K. (2011). Algorithms (4th ed.). Addison-Wesley. Boston.
Thitz, O. (2023). Graafitietokantojen sovelluksia. Systemaattinen kirjallisuuskatsaus. Informaatioteknologian ja viestinnän Pro gradu -tutkielma. Tampereen yliopisto. Tampere.

